Zacznijmy od problemu prostszego: rzutowania promieni.
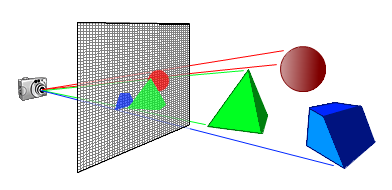
Użyjemy promieni wychodzących z naszego wirtualnego oka (lub kamery)
aby sprawdzać, które obiekty sceny są widoczne w kierunku kolejnych pikseli ekranu.
Jeżeli jakiś obiekt jest widoczny w kierunku promienia od oka do piksela,
rysujemy ten piksel w kolorze znalezionego obiektu.
Jeżeli żaden obiekt nie jest widoczny w tym kierunku, rysujemy czarne tło.
Jest to rzutowanie promieni (ray casting), a nie śledzenie promieni (ray tracing),
gdyż promienie są rzutowane od oka w scenę wirtualną tylko do obliczania widoczność obiektów.
Nie są analizowane: źródła światła, cieniowanie, cienie, odbicia, itd.
Algorytm idzie jak następuje:
dla każdego piksela na ekranie ps
niech v będzie wektorem z naszego wirtualnego oka przez ps
niech dmin (minimalna odległość do elementu) będzie równa max float
niech emin (element sceny najbliższy oku) będzie równy NULL
dla każdego elementu sceny e
niech p będzie punktem przecięcia v i e
jeżeli p istnieje to
niech d będzie odległością p od oka
jeżeli d < dmin to
dmin := d;
emin := e;
koniec;
koniec;
koniec;
jeżeli emin <> NULL to
niech ps będzie koloru emin
wpp
niech ps będzie czarny
koniec;
koniec.
Zatem, jeżeli emin <> NULL, emin wskazuje na ten element sceny wirtualnej,
który jest najbliższy oka (a więc widoczny) w kierunku wektora v.
Nadajemy więc odpowiedniemu pikselowi ekranu kolor elementu emin.
Jednakże, jeżeli emin = NULL, wtedy w kierunku wektora v nie zostały znalezione żadne obiekty,
więc rysujemy domyślny kolor tła (na razie niech to będzie czarny).
Mimo, że jest to tylko rzutowanie promieni, nawet ten prosty algorytm wymaga obudowy
która będzie potrzebna przy implementacji bardziej złożonych obliczeń.
Najpierw, musimy zdecydować, jakiego typu obiekty chcemy umieszczać w naszej wirtualnej scenie.
Z różnych powodów, zacznijmy od scen zawierających jedynie trójkąty.
Inne kształty dodamy w przyszłości, ale wzory stojące za renderingiem trójkątów
przedstawiają podstawowe obliczenia.
Tudzież, z trójkątów można budować bardziej złożone kształty,
a nawet symulować dowolne inne kształty (o ile skorzystamy z wystarczającej liczby wystarczająco małych trójkątów).
Następnie, musimy móc obliczyć punkt przecięcia promienia z trójkątem.
To mając, reszta algorytmu powyżej jest już całkiem banalna.
Przed przejściem do szczegółów, zatrzymajmy się jeszcze na chwilę aby omówić terminologię.
-
Punkt w przestrzeni trójwymiarowej - rzecz prosta.
Trzy wartości typu float przedstawiające położenie punktu w standardowym układzie współrzędnych (x, y, z).
-
Promień w przestrzeni trójwymiarowej to wektor
o punkcie początkowym p1 = (x1, y1, z1) i punkcie końcowym p2 = (x2, y2, z2).
Zakładamy, że kierunek promienia jest od p1 do p2.
-
Wektor to promień z punkcie początkowym p1 = (0, 0, 0).
Zatem, tak naprawdę nie ma istotnej różnicy między wektorami
(które są jednoznacznie zdefiniowane przez ich punkty końcowe) a punktami w przestrzeni trójwymiarowej -
zatem pojęć tych będziemy używać zamiennie.
Wróćmy do przecięcia promieni z trójkątami.
Istnieje wiele różnych sposobów na obliczanie takiego przecięcia,
jednak powinniśmy wybrać te, które wymagają jak najmniejszej liczby obliczeń
(zwróćmy uwagę, że powyższy algorytm sprawdza w sumie #pikseli x #trójkątów przecięć).
Intersections of Rays, Segments, Planes and Triangles in 3D przedstawia wymagane algorytmy.
Nie będę tutaj opisywał ich szczegółów (jako że w artykule jest to wystarczająco dobrze zrobione),
jednak zwróćmy tylko uwagę na dwa główne kroki procesu:
- Znajdujemy przecięcie promienia z płaszczyzną, w której leży trójkąt.
- Jeżeli taki punkt istnieje, sprawdzamy, czy punkt ten leży wewnątrz trójkąta.
Implementacja powyższego nie powinna być trudna (po lekturze załączonego artykułu).
Przed ściągnięciem źródeł, może należy jeszcze wyjaśnić kilka drobiazgów:
-
Nie została zdefiniowana klasa "punkt";
wektory zostały zdefiniowane jako pojedyncze punkty (punkt początkowy jest znany).
Można korzystać z wektorów gdziekolwiek potrzebne są punkty.
-
Tak naprawdę nie obliczamy odległości, a kwadrat odległości.
Ponieważ szukamy tylko najbliższego obiektu, nie musimy wyniku przekazywać do (czasochłonnej) funkcji sqrt().
-
Niekiedy, do porównania dwóch punktów / wektorów korzystam z małej wartości (EPSILON).
Problem leży w immanentnej niedokładności obliczeń zmienno-przecinkowych.
Rozwiązaniem nie jest porównywanie dokładnych wartości, a ich przybliżeń
(które jednak muszą być wystarczająco dokładne; stąd EPSILON zdefiniowane jest jako 1e-10).
-
Właśnie, korzystamy z typu float miast typu double, gdyż duża dokładność nie jest tak bardzo ważna w renderingu scen.
Za to prędkość obliczeń jest (i to bardzo).
-
Klasa "engine" przeprowadza obliczenia renderingu;
Canvas->Pixels[x][y] jest dosyć wolne (zabiera około połowy czasu renderingu sceny poniżej),
ale gdy zaczniemy komplikować algorytm, rzecz przestanie być istotnym problemem.
-
Klasa "scene" odpowiedzialna jest za obsługę obiektów należących do renderowanej sceny.
Ma też metody generowania scen.
TYRTScene::GenerateExample_01Triangles zostały użyta do utworzenia obrazka poniżej.
No dobra, po całym tym wstępie, wypróbujmy algorytm na prostym przykładzie:
Niezbyt to skomplikowana scena, ale jest to już jakiś początek!
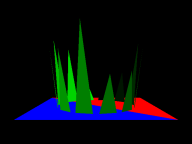
Niezbyt to skomplikowana scena, ale jest to już jakiś początek!
A źródła (projekt C++Builder) do powyższego można znaleźć
tutaj.
Góra
|